2022-07-10
접근 방법
가 최소가 되는 T의 개수를 구하는 문제입니다
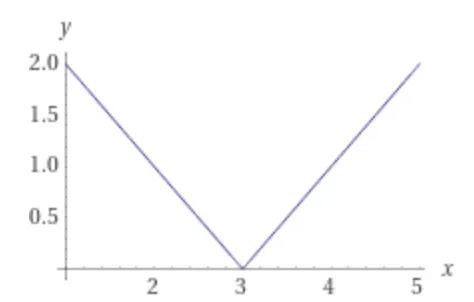
•
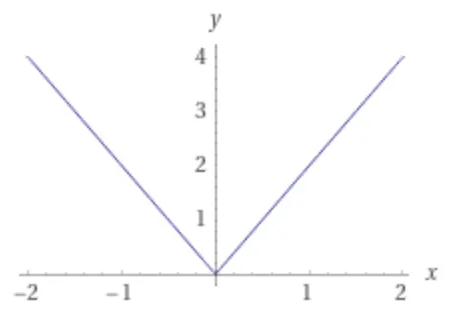
이 최소값이 되는 x는 [3]으로 한 개입니다
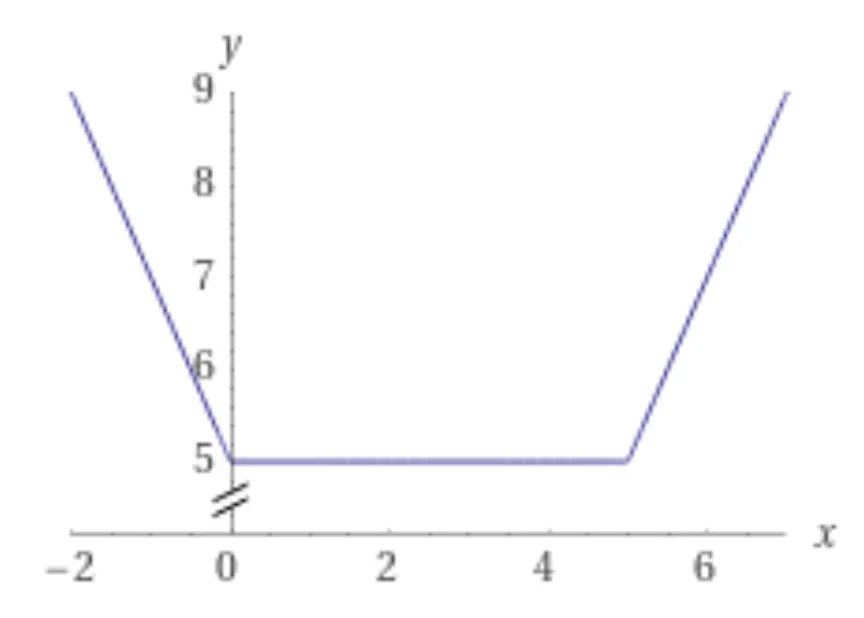
•
이 최소값이 되는 x는 [0, 1, 2, 3, 4, 5]로 5개 입니다
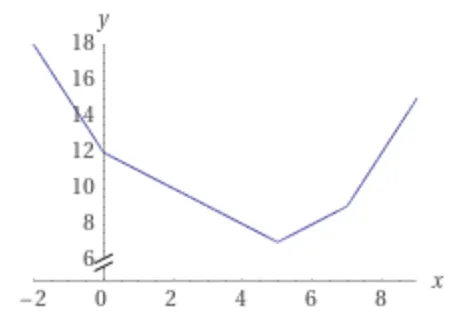
•
이 최소값이 되는 x는 [5]로 한 개 입니다
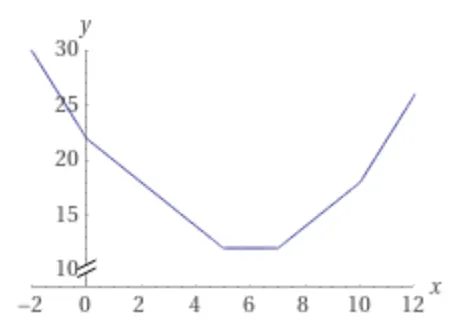
•
이 최소값이 되는 x는 [5, 6, 7]로 3개 입니다
규칙성이 보이시나요?
1차식, 3차식과 같은 홀수 차식에서는 최소값이 되는 값은 항상 1개입니다
그리고 2차식, 4차식과 같은 짝수 차식에서는 오름차순으로 x 절편을 정렬했을 때 중앙의 두 값을 포함한 사이 값들이 최소값이 되는 값들입니다.
•
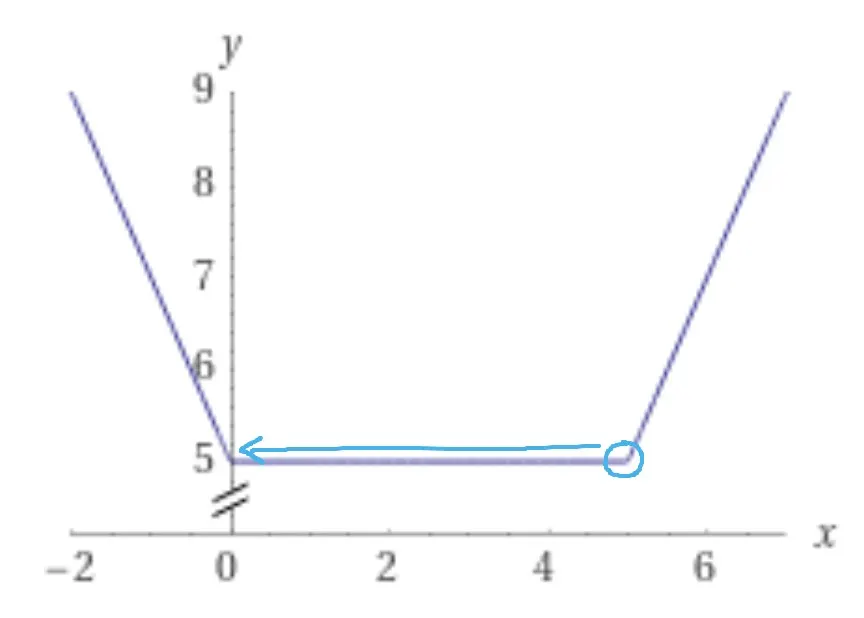
y = |x| + |x-5| 에서 오름차순으로 정렬한 x 절편들은 [0, 5] 입니다. 여기에서 중앙의 두 값을 포함한 사이의 값 0~5가 모두 y가 최소가 되는 값들입니다.
•
y = |x| + |x-5| + |x-7| + |x-10| 에서 오름차순으로 정렬한 x의 절편들은 [0, 5, 7, 10] 입니다. 여기에서 중앙의 두 값을 포함한 사이의 값은 5~7이 모두 y가 최소가 되는 값들입니다.
마지막으로 다음과 같은 엣지 케이스입니다.
는 그래프상에서 y = |x| + |x-5| 의 그래프에서 x=5 포인트가 오른쪽으로 이동했다고 생각하면 됩니다.
이 엣지 케이스의 접근 방법은 짝수 차식의 접근 방법과 동일합니다. 오름차순으로 정렬한 x 절편들은 [0, 0] 입니다. 여기에서 중앙의 두 값을 포함한 사이값 0~0으로 1개가 최소가 되는 값입니다.
그래서 문제 풀이에서는 엣지 케이스를 따로 처리할 필요가 없습니다.
수학적인 지식이 있으면 좀 더 문제를 쉽게 풀 수 있다고 생각합니다. 저 또한 위의 내용들을 바로 안 것이 아니고 10분 정도 그래프 개형을 공책에 그리면서 위에서 서술한 접근 방식을 알게 되었습니다.
파이썬 코드
import sys
input = sys.stdin.readline
n = int(input())
numbers = list()
for _ in range(n):
a, b = map(int, input().split())
numbers.append(b - a)
numbers = sorted(numbers)
answer = 0
if len(numbers) % 2 == 0:
start = len(numbers) // 2 - 1
answer = numbers[start + 1] - numbers[start] + 1
else:
answer = 1
print(answer)
Python
복사