2022-07-10
플로이드-워셜 알고리즘을 기록으로 남깁니다.
나동빈님의 유튜브 영상을 보며 공부하였습니다.
플로이드-워셜 알고리즘 설명
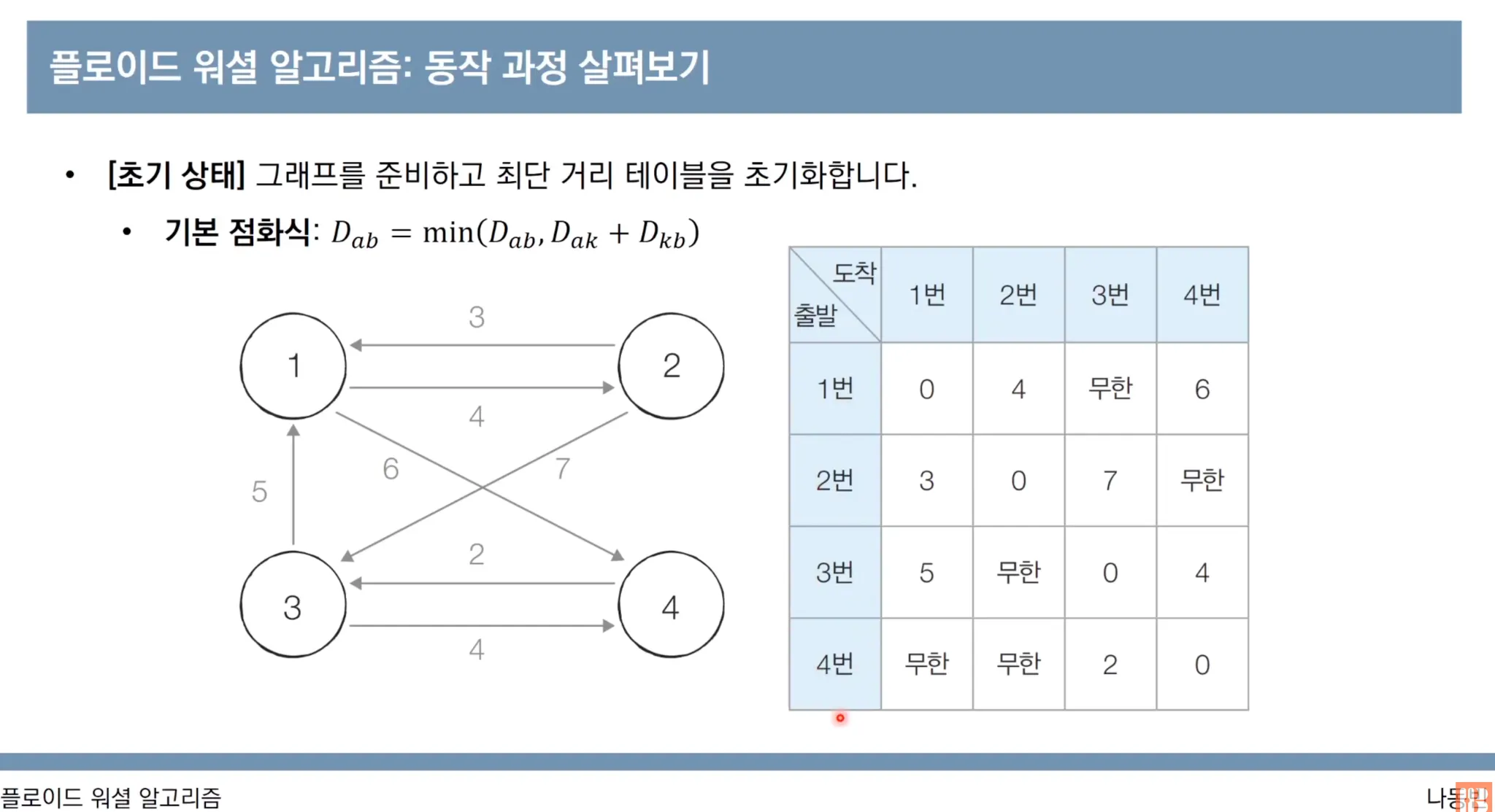
플로이드-워셜 알고리즘은 a → b로 가는 비용과 a → k → b로 가는 비용 중 더 적은 것을 최단 거리로 설정합니다. 그래서 다음과 같은 점화식을 만들 수 있습니다
동작 과정
행(row)은 출발점, 열(column)은 도착점인 2차원 행렬을 만듭니다.
그리고 a → b로 가는 경로의 초기 비용을 설정합니다.
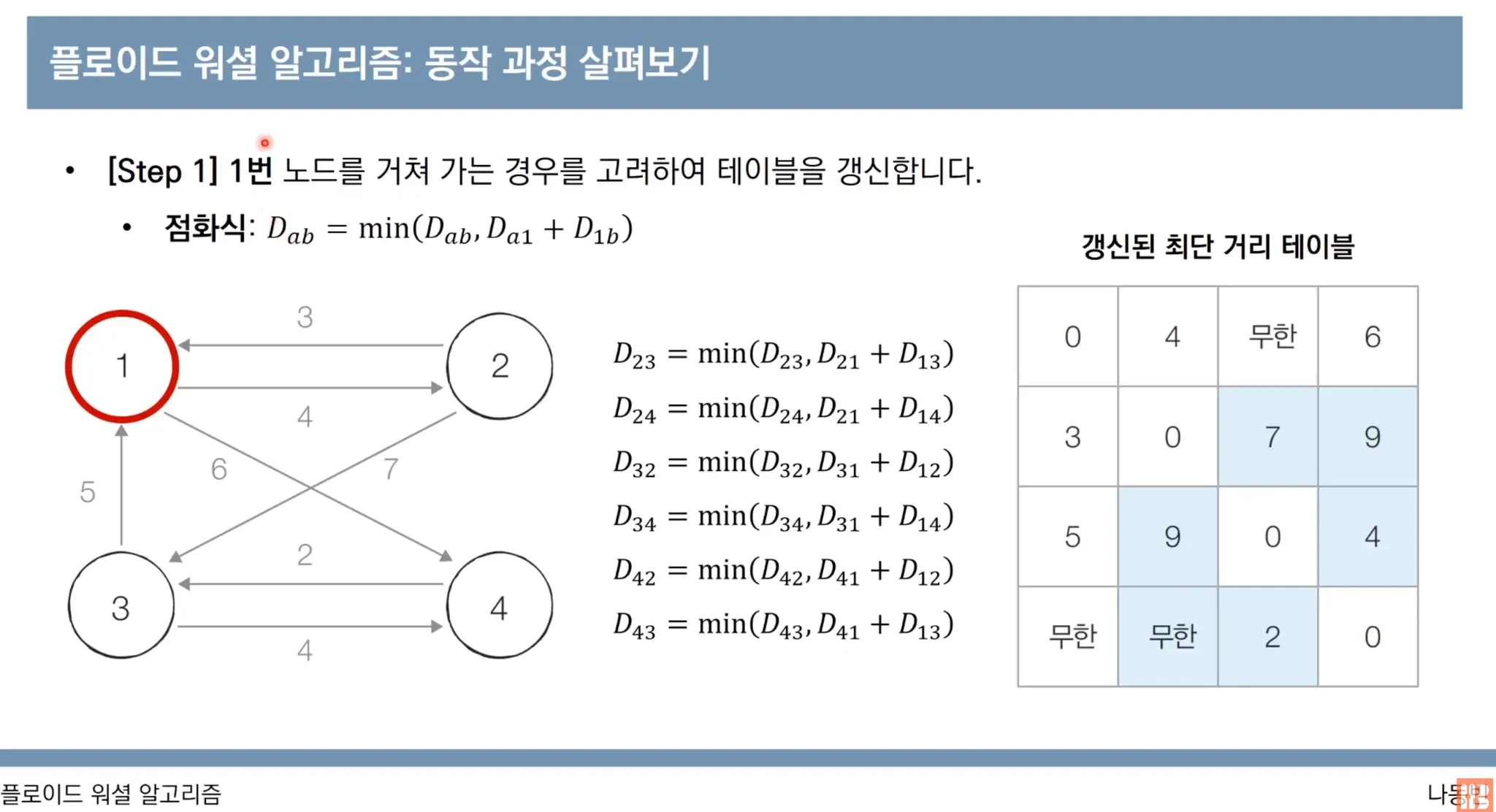
그리고 1번 노드를 거쳐 가는 경우에 min(a → b, a → 1 → b)를 계산하여 행렬을 갱신합니다.
a → 1 → b로 가는 경우는 1번 노드 자기 자신을 제외한 총 3개의 노드에서 3 x 2 = 6가지 입니다.
그래서 2차원 행렬에서 파란색으로 표시된 갱신 가능한 부분은 6군데 입니다.
예를 들어, 3번 → 1번 → 2번 노드로 가는 비용은 5 + 4 = 9 입니다. 3번 → 2번 노드로 바로 가는 경우는 없기(무한) 때문에 9로 업데이트 되었습니다.
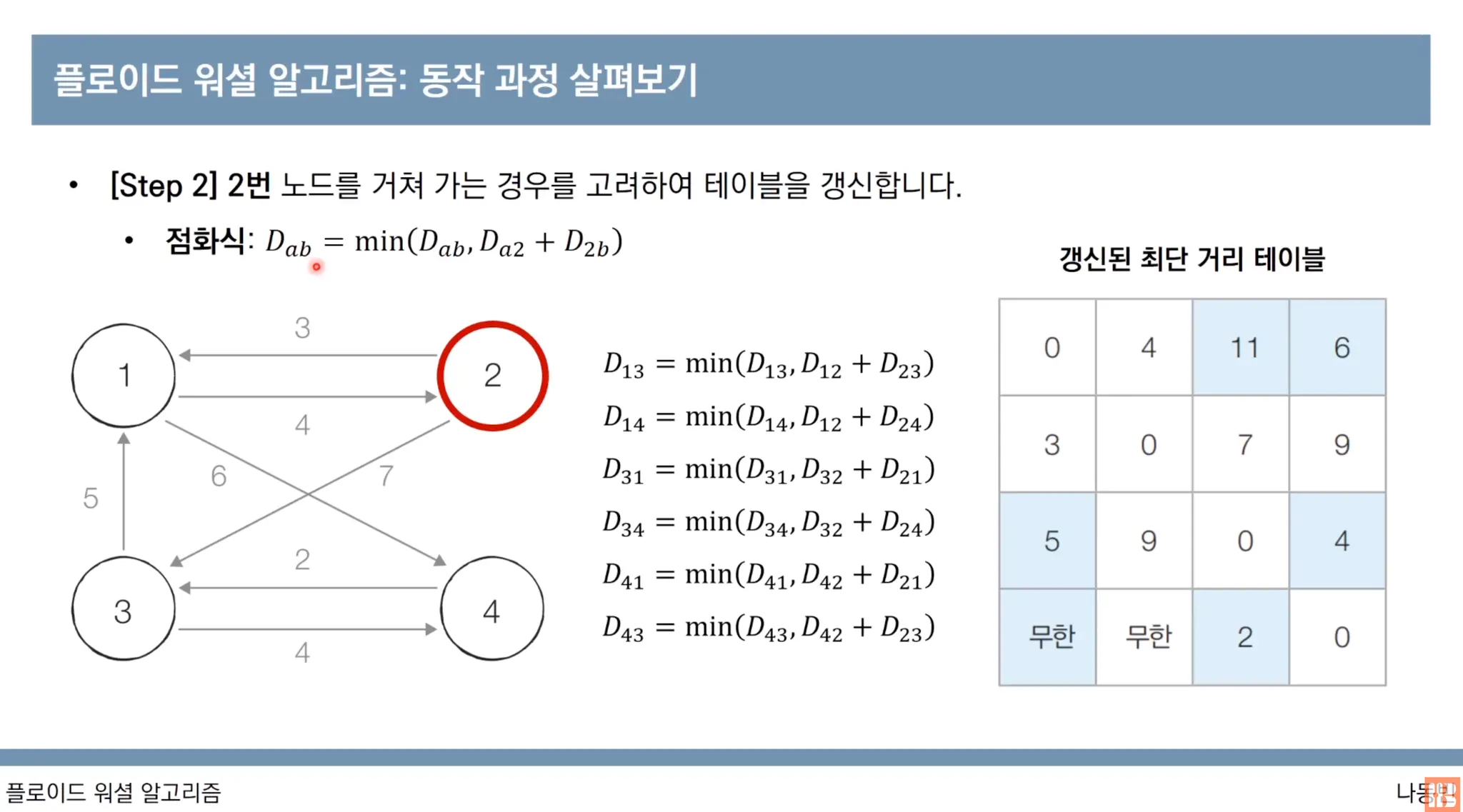
이 과정을 반복하여 이번에는 2번 노드를 거쳐 가는 경우에도 행렬을 업데이트 합니다.
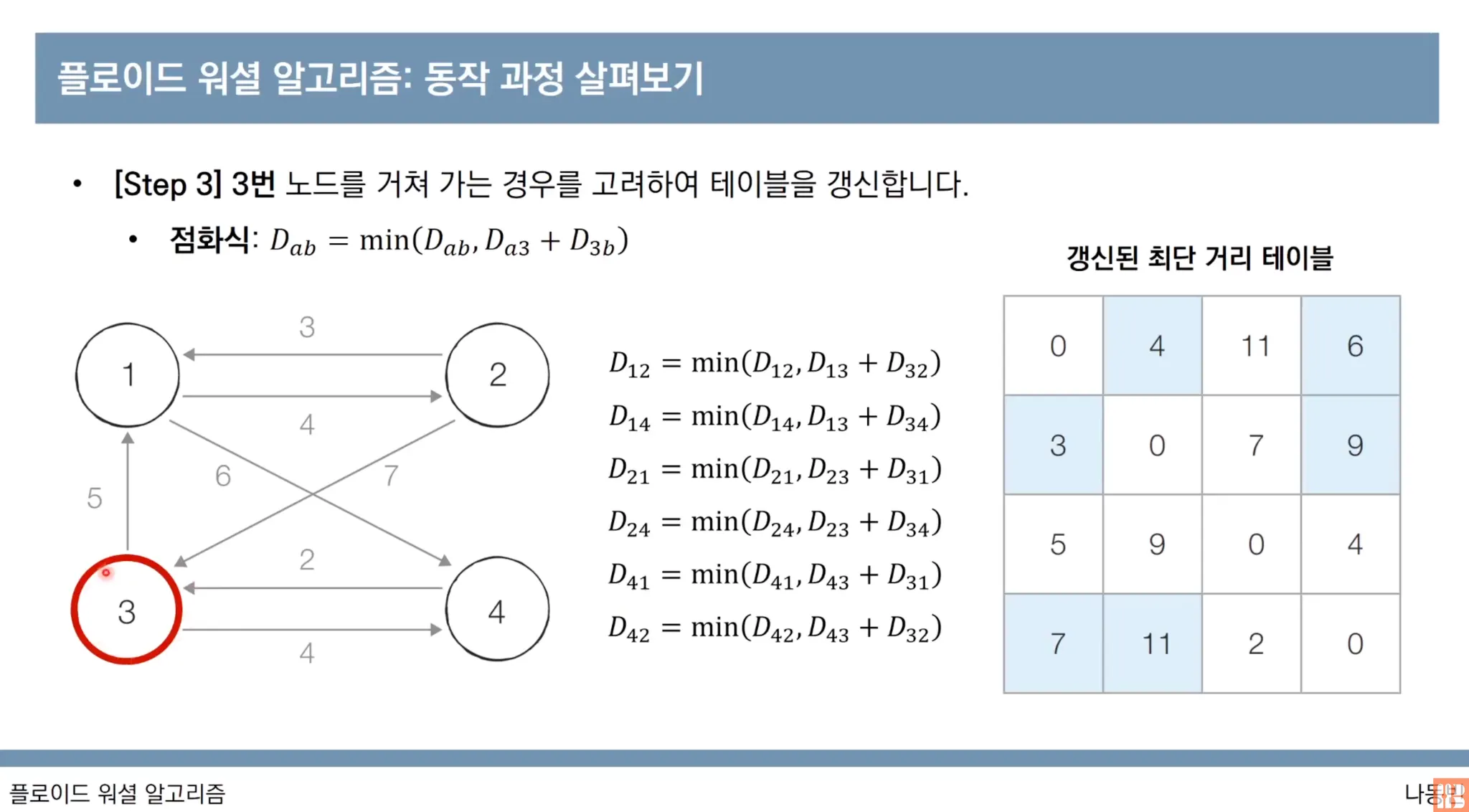
3번 노드를 거쳐 가는 경우의 행렬 업데이트 과정을 진행합니다.
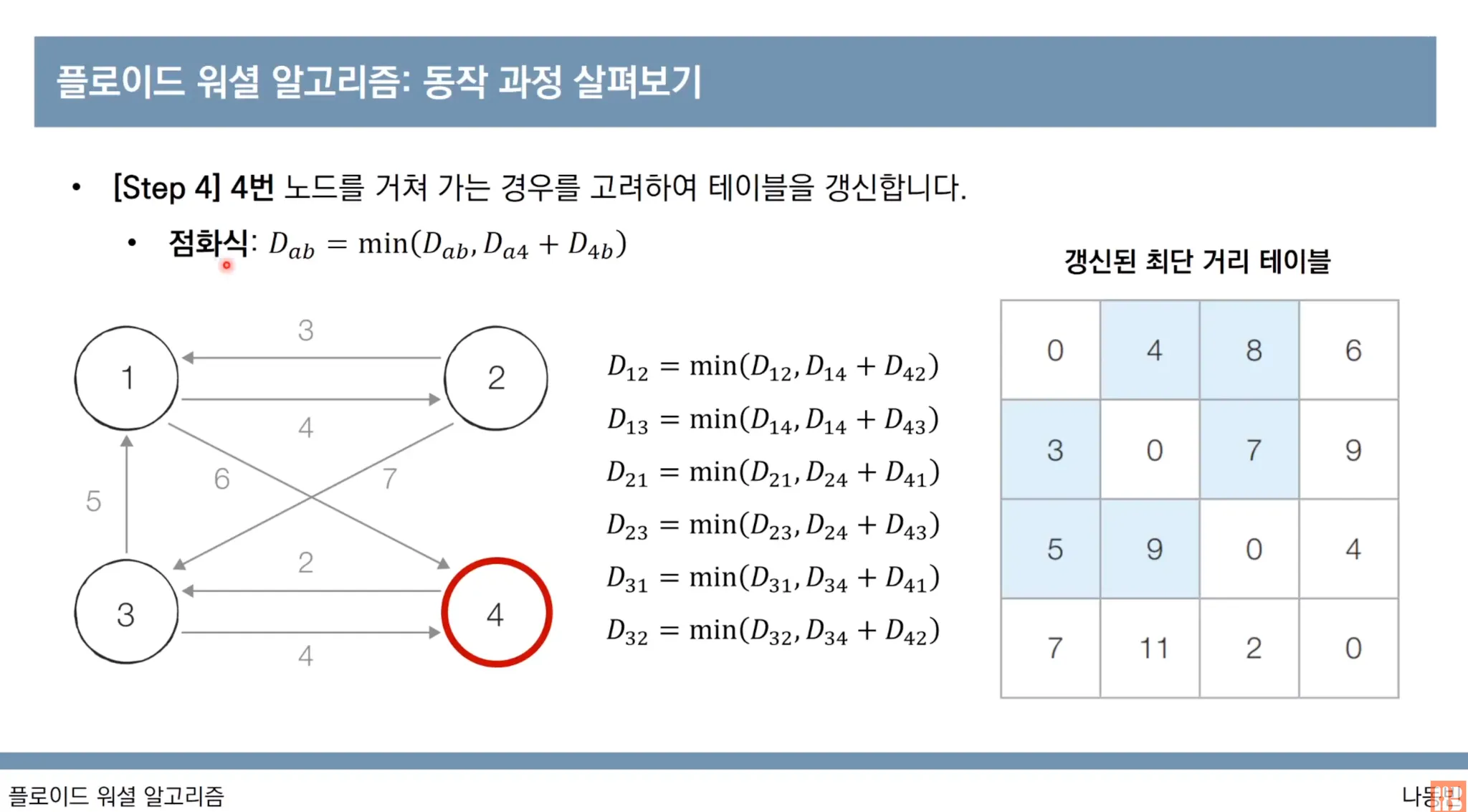
4번 노드를 거쳐 가는 경우의 행렬 업데이트 과정을 진행합니다.
플로이드-워셜 알고리즘 성능
이 과정을 보면 대략적인 알고리즘 흐름을 알 수 있습니다.
# 전체적인 과정
(for문) k번 노드를 거쳐 가는 과정
min(a → b, a → k → b)
# 여기에서 min(a → b, a → k → b)을 계산할 때 2차원 행렬이기 때문에 2중 반복문을 사용하게 됩니다.
# 풀어쓴 전체적인 과정
(for문) k번 노드를 거쳐 가는 과정
(for문) 행(row) 탐색
(for문) 열(column) 탐색
min(row -> column, row -> k -> column)
Python
복사
따라서 플로이드-워셜 알고리즘의 시간복잡도는 O(n^3) 입니다
최단거리 문제가 출제되었을 때 다익스트라, 플로이드-워셜 등의 알고리즘 중에서 어떤 것이 더 적절한 지 판단해야 합니다.
•
플로이드-워셜로 N이 500인 문제를 푼다고 가정했을 때, 500 * 500 * 500 > 1.2억이 넘어가기 때문에 느립니다. 시간 초과가 날 수 있습니다.
파이썬 코드로 구현
INF = int(1e9) # 무한을 10억으로 설정
# 노드의 개수 및 간선의 개수 입력 받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프)를 만들고 무한으로 초기화
graph = [[INF] * (1 + n) for _ in range(n + 1)]
# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for i in range(1, n + 1):
graph[i][i] = 0
# 각 간선에 대한 정보를 받아 그 값으로 초기화
for _ in range(m):
a, b, c = map(int, input().split())
graph[a][b] = c
# 점화식에 따라 플로이드 워셜 알고리즘 수행
for k in range(1, n + 1): # k를 거쳐 가는 경우
for a in range(1, n + 1):
for b in range(1, n + 1):
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])
# 수행된 결과를 출력
for a in range(1, n + 1):
for b in range(1, n + 1):
# 도달할 수 없는 경우, 무한(INF)으로 출력
if graph[a][b] == INF:
print("INF", end=" ")
else:
print(graph[a][b], end=" ")
print()
Python
복사