2022-07-23
접근 방식
전형적인 점화식을 찾는 Dynamic Programming 문제입니다.
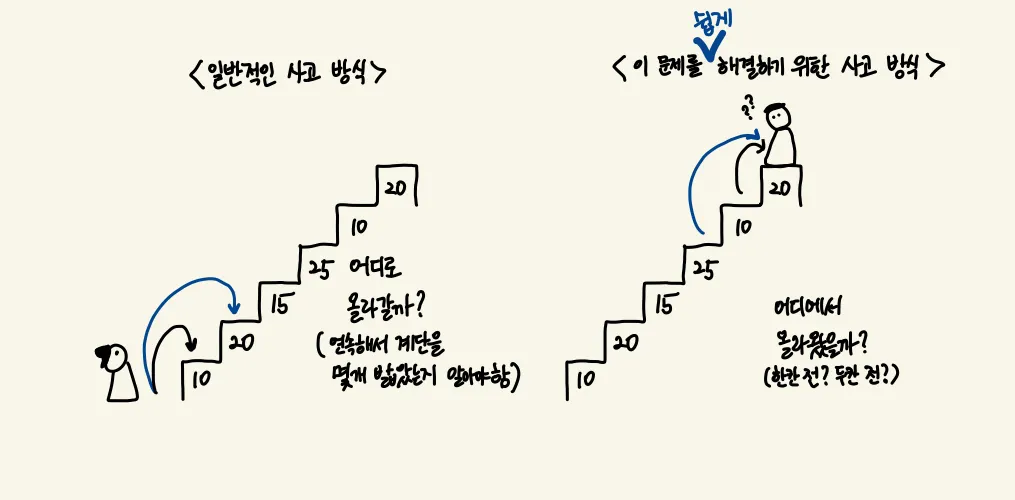
이 문제에서 점화식을 찾을 때 3번 규칙 (마지막 도착 계단은 반드시 밟아야 한다) 따라야하기 때문에 점화식을 계단을 올라가는 앞에서 생각하는 방식보다는 도착지부터 생각하는 방식의 접근이 더 쉽습니다.
dp[n]은 n번째 계단에 올랐을 때 얻을 수 있는 점수의 최댓값입니다.
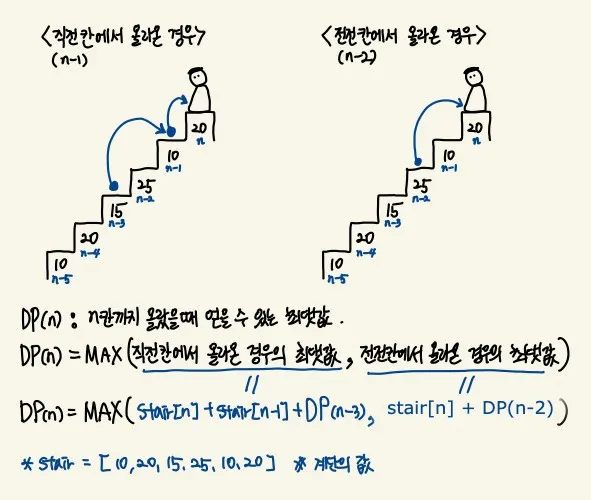
n 번째 계단에 올라오기 위해서는 두 가지 경우가 있습니다. n-1번째 계단으로 오는 경우와 n-2번째 계단으로 오는 경우입니다.
1.
n-1번째 계단으로 오는 경우에는
dp[n] = dp[n-3] + stairs[n-1] + stairs[n] 입니다
2.
n-2번째 계단으로 오는 경우에는
dp[n] = dp[n-2] + stairs[n] 입니다
이 중에서 더 큰 수가 dp[n]이 됩니다.
점화식에서 보면 첫번째 식에서 dp[n-3]이 있기 때문에 1, 2, 3층의 dp는 초기화해주어야 합니다.
파이썬 코드
import sys
input = sys.stdin.readline
n = int(input())
# 계단의 숫자를 초기화 합니다. 1층은 1번째(not 0번째) 인덱스에 저장합니다.
stairs = [0] * 301
for i in range(1, n + 1):
stairs[i] = int(input())
# dp 배열을 초기화합니다.
dp = [0] * 301
dp[1] = stairs[1]
dp[2] = stairs[1] + stairs[2]
dp[3] = max(stairs[1] + stairs[3], stairs[2] + stairs[3])
# 점화식을 계산합니다.
for i in range(4, n + 1):
dp[i] = max(dp[i - 3] + stairs[i - 1] + stairs[i], dp[i - 2] + stairs[i])
print(dp[n])
Python
복사
이 코드는 먼저 작은 문제인 계단 한 칸, 두 칸 또는 세 칸을 오르는 경우에 대해 답을 구하고, 이를 활용하여 큰 문제인 n칸을 오르는 경우에 대한 답을 구하는 방식(Bottom up 방식)으로 문제를 해결하였습니다